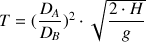Conservation de l'énergie mécanique : loi de Bernoulli
La loi de Bernoulli traduit la conservation de l'énergie mécanique d'un fluide qui s'écoule entre deux sections d'une conduite.
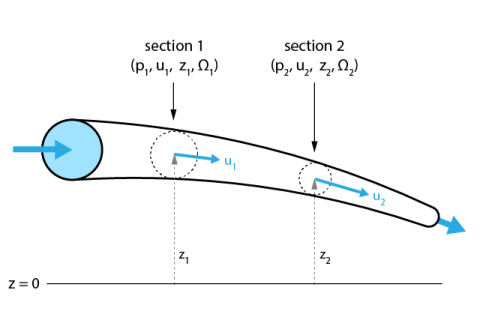
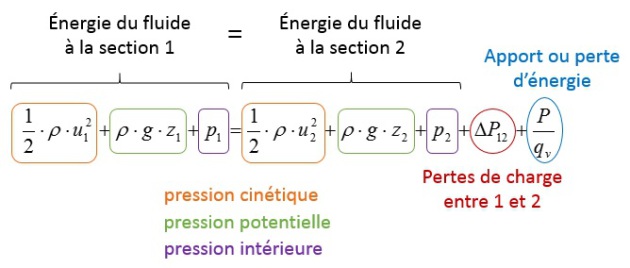
L'énergie mécanique du fluide se décompose en trois catégories : l'énergie cinétique, l'énergie potentielle et l'énergie de pression. Dans l'équation proposée ci-dessous, ces énergies sont exprimées sous forme de pression (pression cinétique, pression potentielle et pression intérieure).
Deux termes peuvent moduler l'égalité de l'énergie mécanique entre les sections 1 et 2 :
les pertes de charge exprimée sous forme de pression (en Pa) ; le calcul des pertes de charge sera abordé dans la suite du cours
l'apport ou la perte d'énergie via un organe présent sur la conduite entre les sections 1 et 2 ; par exemple, la présence d'une pompe se traduira par un apport d'énergie au fluide (P>0), alors qu'une turbine prendra de l'énergie au fluide (P<0) ; cet apport ou perte d'énergie est exprimé sous forme d'une puissance divisée par le débit volumique de fluide, ce qui correspond à une pression (en Pa)
S'il n'y a pas de pertes de charge (négligée, considérant un fluide parfait à viscosité nulle) et aucun organe apportant ou prenant de l'énergie au fluide, l'équation de Bernoulli se simplifie comme suit :
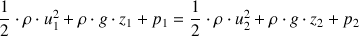
rho : masse volumique du fluide (kg.m-3)
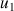: vitesse du fluide au niveau de la section 1 (m.s-1)
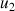: vitesse du fluide au niveau de la section 2 (m.s-1)
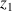: altitude de la section 1 (au centre) (m)
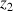: altitude de la section 2 (au centre) (m)
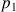: pression du fluide au niveau de la section 1 (Pa)
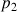: pression du fluide au niveau de la section 2 (Pa)
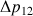: pertes de charge éventuelles entre les sections 1 et 2 (Pa)
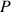: puissance éventuellement apportée ou prise au fluide par un organe placé sur la conduite (W)
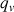: débit volumique du fluide (m3.s-1)
Quelques exemples d'applications de la loi de Bernoulli sont donnés ci-après.
Application à la mesure de vitesse : tube de Pitot
Le tube de Pitot est un système de mesure de la vitesse d'un fluide. Le principe est de mesurer la différence de pression entre deux prises de pressions :
une prise de pression statique dont l'axe est perpendiculaire à l'écoulement du fluide (point A sur le schéma)
une prise de pression dynamique dont l'axe est parallèle à l'écoulement du fluide (point B sur le schéma)
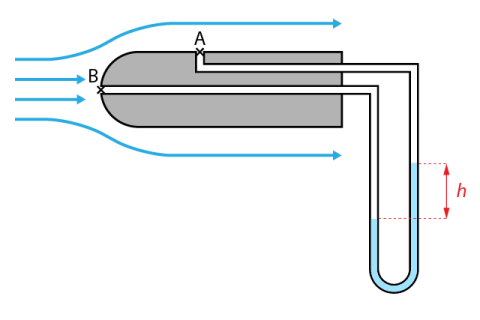
Si l'on fait l'hypothèse de l'absence de pertes de charge entre les points A et B, et que les points A et B sont à la même hauteur (
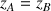), l'équation de Bernoulli entre les points A et B s'écrit comme suit :
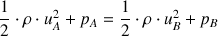
D'autre part, on peut considérer que uB=0 car le fluide est stoppé au niveau du point B par la présence du tube de Pitot. On a alors :
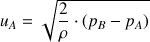
Si on considère un manomètre à tube en U (contenant un fluide de masse volumique
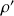), on peut exprimer la différence de pression en fonction de la dénivellation
:
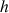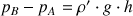
Finalement, la vitesse du fluide s'exprime comme suit :
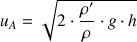
Application à la mesure de débit : Venturi
Un Venturi est un système permettant de mesurer le débit d'un fluide. Il consiste en un tube avec un rétrécissement. Le principe est de mesurer la différence de pression entre les sections de grand et petit diamètre.
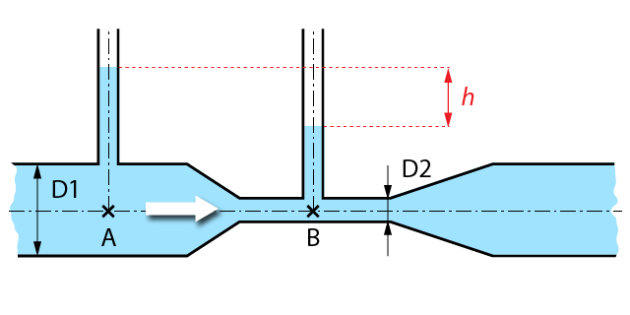
XXX l'image ne correspond pas à l'image fournie
L'application de la loi de Bernoulli permet d'exprimer le lien entre vitesse du fluide et pression entre les points A et B (dans ce cas
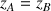, et on néglige les pertes de charge) :
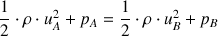
Les vitesses peuvent être exprimées en fonction du débit volumique et du diamètre du tube :
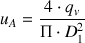
et :
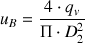
Ainsi, le débit volumique du fluide s'exprime :
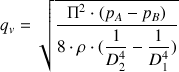
Si la différence de pression entre les points A et B est déterminée par un système de tube en U, avec une dénivellation
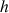, on obtient finalement :
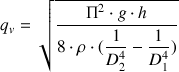
Application à la vidange d'une cuve
On considère une cuve cylindrique de diamètre
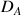initialement remplie d'une hauteur
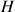d'eau. Cette cuve peut être vidangée par un orifice de diamètre
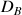situé au bas de la cuve.
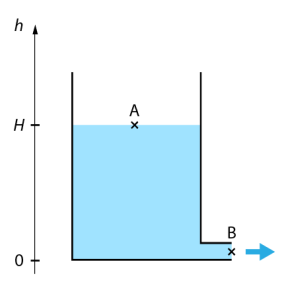
En considérant que le fluide est parfait (pas de pertes de charge), que les pressions au points A et B sont égales (pression atmosphérique), et que la vitesse au point A est négligeable par rapport à celle au point B, la loi de Bernoulli permet d'exprimer la vitesse du fluide au point B à un instant t en fonction de la hauteur de fluide dans la cuve :
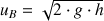
La vitesse du fluide au point A peut d'autre part être exprimée comme suit :
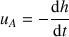(attention au signe)
En partant de l'égalité des débits aux points A et B, on peut écrire :
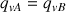
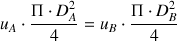
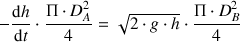
Après intégration de cette expression entre les temps t=0 et t=T et les hauteurs h=H et h=0, on obtient finalement l'expression du temps nécessaire à la vidange de la cuve
:
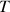