Statique des fluides
La statique des fluides concerne l'étude des fluides au repos (qui ne s'écoulent pas). Elle est régie par le principe fondamental de l'hydrostatique, dont l'application principale en génie des procédés porte sur la mesure de pressions.
Le principe fondamental de la statique des fluides
Le principe fondamental de la statique des fluides (ou principe fondamental de l'hydrostatique, ou principe de Pascal) établit les points suivants :
La pression au sein d'un fluide statique dépend de la profondeur ; en tout point d'un même plan horizontal, la pression est identique. Dans l'hypothèse d'un fluide incompressible, le fluide transmet intégralement les efforts ; ainsi, la pression en un point A situé à une profondeur
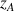 résulte de la pression qu'exerce l'air en surface (
résulte de la pression qu'exerce l'air en surface (
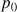 ) et de la pression (poids par unité de surface) exercée par la colonne de liquide au-dessus du point A (
) et de la pression (poids par unité de surface) exercée par la colonne de liquide au-dessus du point A (
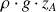 ).
).
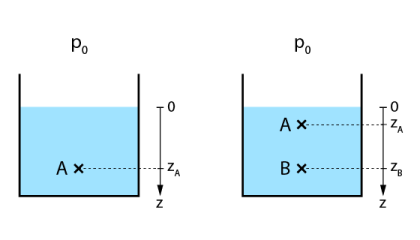
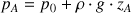
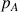 : pression au point A (Pa)
: pression au point A (Pa)
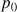 : pression au sein de l'air en surface (Pa)
: pression au sein de l'air en surface (Pa)
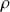 : masse volumique du fluide (kg.m-3)
: masse volumique du fluide (kg.m-3)
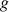 : accélération de la pesanteur (g=9.81 m.s-2)
: accélération de la pesanteur (g=9.81 m.s-2)
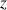 : profondeur du point A (m)
: profondeur du point A (m)
De même, on peut exprimer la différence de pression entre 2 points A et B à différentes profondeurs au sein d'un fluide comme suit :
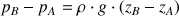
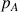 : pression au point A (Pa)
: pression au point A (Pa)
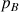 : pression au point B (Pa)
: pression au point B (Pa)
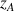 : profondeur du point A (m)
: profondeur du point A (m)
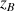 : profondeur du point B (m)
: profondeur du point B (m)
Application à la mesure des pressions
La mesure de pression est réalisée avec des appareils appelés manomètres. Le manomètre est placé sur une prise de pression (orifice en contact avec le fluide), qui peut être statique (perpendiculaire à l'axe de l'écoulement) pour mesurer la pression du fluide, ou dynamique (face à l'écoulement) pour mesurer à la fois la pression du fluide et la pression cinétique liée à sa vitesse. Dans tous les cas, la prise de pression doit être placée de manière à perturber le moins possible l'écoulement du fluide.
Dans les procédés industriels, deux grands types de manomètres sont principalement utilisés : les manomètres mécaniques et les manomètres à tube en U.
Le manomètre mécanique consiste en un cadran gradué avec une aiguille indiquant la pression. Le principe est celui d'une pièce élastique (diaphragme, tube courbé) reliée d'un côté à la prise de pression et de l'autre à l'aiguille, qui va se déformer en fonction de la pression, et engendrer un déplacement de l'aiguille sur le cadran.
Le manomètre à tube en U consiste en un tube en forme de U dans lequel est placé un liquide de masse volumique connue. Une extrémité du tube en U est relié à une prise de pression, l'autre est reliée à une autre prise de pression ou à l'air ambiant. En fonction de la pression exercée à chaque extrémité du tube en U, le liquide se déplace préférentiellement dans l'une ou l'autre branche du tube en U, induisant une certaine dénivellation (h). La mesure de cette dénivellation permet de calculer la pression en un point (ou différence de pression entre 2 points), en appliquant le principe fondamental de la statique des fluides.
NB : le fluide placé dans le tube en U doit être immiscible avec le fluide circulant dans la conduite. Il est en général coloré de manière à bien le distinguer et faciliter la lecture de la dénivellation.
Cas de la mesure de pression en 1 point
Soit une conduite dans laquelle circule un fluide de masse volumique
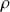 . En un point A de la conduite, se trouve une prise de pression, à laquelle on raccorde l'une des branches d'un manomètre à tube en U rempli d'un liquide de masse volumique
. En un point A de la conduite, se trouve une prise de pression, à laquelle on raccorde l'une des branches d'un manomètre à tube en U rempli d'un liquide de masse volumique
 . La 2ème branche du tube en U est reliée à l'air ambiant. On mesure une dénivellation h dans le tube en U.
. La 2ème branche du tube en U est reliée à l'air ambiant. On mesure une dénivellation h dans le tube en U.
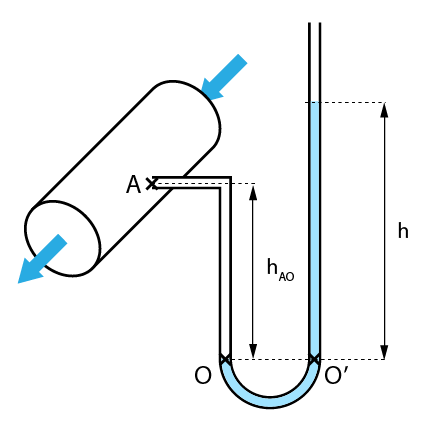
Afin de connaître la pression
 au point A, on applique le principe fondamental de la statique des fluides.
au point A, on applique le principe fondamental de la statique des fluides.
Les points O et O' se trouvant sur un même plan horizontal, leur pression est identique. D'autre part, on peut exprimer les pressions aux points O et O' en déterminant les pressions exercées par les colonnes de fluides au-dessus de ces 2 points :
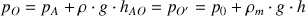
D'où :
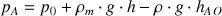
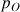 : pression au point O (Pa)
: pression au point O (Pa)
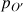 : pression au point O' (Pa)
: pression au point O' (Pa)
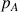 : pression au point A (Pa)
: pression au point A (Pa)
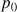 : pression atmosphérique (de l'air ambiant) (Pa)
: pression atmosphérique (de l'air ambiant) (Pa)
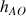 : distance entre les points A et O (m)
: distance entre les points A et O (m)
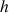 : dénivellation dans le tube en U (m)
: dénivellation dans le tube en U (m)
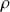 : masse volumique du fluide circulant dans la conduite (kg.m-3)
: masse volumique du fluide circulant dans la conduite (kg.m-3)
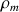 : masse volumique du fluide dans le tube en U (kg.m-3)
: masse volumique du fluide dans le tube en U (kg.m-3)
Si le fluide circulant dans la conduite est un gaz (masse volumique faible), on pourra alors négliger la pression exercée par la colonne de gaz. On obtient alors :
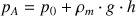
Cas de la mesure d'une différence de pression entre 2 points
Soit une conduite dans laquelle circule un fluide de masse volumique
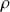 . On raccorde les deux branches d'un manomètre à tube en U entre deux points de la conduite A et B. Le tube en U est rempli d'un liquide de masse volumique
. On raccorde les deux branches d'un manomètre à tube en U entre deux points de la conduite A et B. Le tube en U est rempli d'un liquide de masse volumique
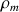 . On mesure une dénivellation h dans le tube en U.
. On mesure une dénivellation h dans le tube en U.
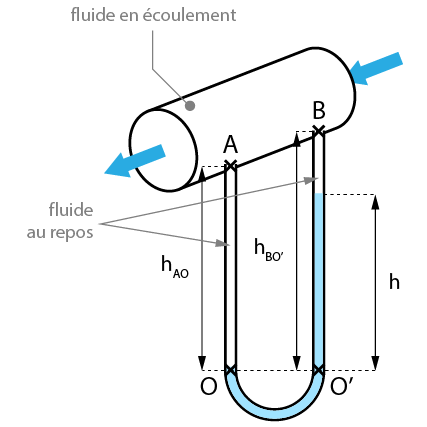
De même que dans le cas précédent, les points O et O' se trouvent sur un même plan horizontal, donc leur pression est identique. On peut exprimer les pressions aux points O et O' en appliquant le principe fondamental de la statique des fluides :
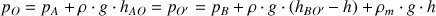
D'où :
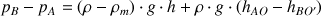
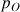 : pression au point O (Pa)
: pression au point O (Pa)
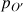 : pression au point O' (Pa)
: pression au point O' (Pa)
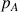 : pression au point A (Pa)
: pression au point A (Pa)
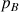 : pression au point B (Pa)
: pression au point B (Pa)
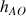 : distance entre les points A et O (m)
: distance entre les points A et O (m)
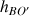 : distance entre les points B et O' (m)
: distance entre les points B et O' (m)
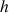 : dénivellation dans le tube en U (m)
: dénivellation dans le tube en U (m)
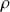 : masse volumique du fluide circulant dans la conduite (kg.m-3)
: masse volumique du fluide circulant dans la conduite (kg.m-3)
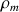 : masse volumique du fluide dans le tube en U (kg.m-3)
: masse volumique du fluide dans le tube en U (kg.m-3)
Si la conduite est horizontale, on a
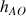 =
=
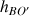 , et l'expression se simplifie comme suit :
, et l'expression se simplifie comme suit :
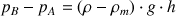
NB : Dans ces dispositifs de manomètre à tube en U, la continuité entre les fluides doit être assurée pour que les pressions soient transmises intégralement d'un fluide à l'autre. Ainsi, il est nécessaire de réaliser régulièrement des purges pour chasser les éventuelles bulles d'air.





