Écoulement laminaire en conduite cylindrique : loi de Poiseuille
En mécanique des fluides, le mouvement des fluides Newtoniens est décrit par les équations de Navier-Stokes (équations aux dérivées partielles non linéaires, valables dans des milieux continus). La résolution de ces équations complexes est difficile et nécessite la plupart du temps d'adopter des hypothèses simplificatrices.
La résolution de ces équations dans le cas de l'écoulement d'un fluide Newtonien incompressible en régime laminaire aboutit à la loi ou équation de Poiseuille :
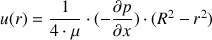
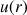: vitesse du fluide au rayon r (m.s-1)
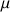: viscosité dynamique du fluide (Pa.s)
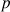: pression (Pa)
: abscisse (suivant l'axe parallèle à la conduite) (m)
: rayon (coordonnée cylindrique) (m)
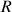: rayon interne de la conduite (m)
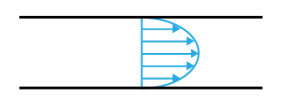
L'équation de Poiseuille donne la vitesse du fluide en fonction du rayon auquel on se place dans la conduite. Elle traduit le profil parabolique des vitesses.
A partir de cette équation, on peut exprimer la vitesse moyenne du fluide au sein de la conduite sur une longueur L donnée :
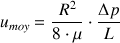
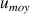: vitesse moyenne du fluide (m.s-1)
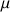: viscosité dynamique du fluide (Pa.s)
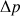: gradient de pression sur la longueur de conduite L (Pa)
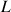: longueur de conduite considérée (m)
